Квадрат по четырём точкам
Apr. 14th, 2017 05:00 pm![[personal profile]](https://www.dreamwidth.org/img/silk/identity/user.png){kind=small}
dimviewЗадачка: построить квадрат по четырём точкам (по одной точке с каждой стороны квадрата).
То есть кто-то начертил квадрат, поставил на каждой стороне по одной точке (неизвестно в каком месте), потом квадрат стёр, но точки оставил. Задача — восстановить квадрат (найти его углы), используя обычные геометрические построения циркулем и линейкой.
Никаких подвохов, всё честно, для решения достаточно знания геометрии на уровне очень средней школы. Простое решение, которое сложно найти — под катом.
Выбираем две противоположные точки (в этом примере B и D) и соединяем их прямой.
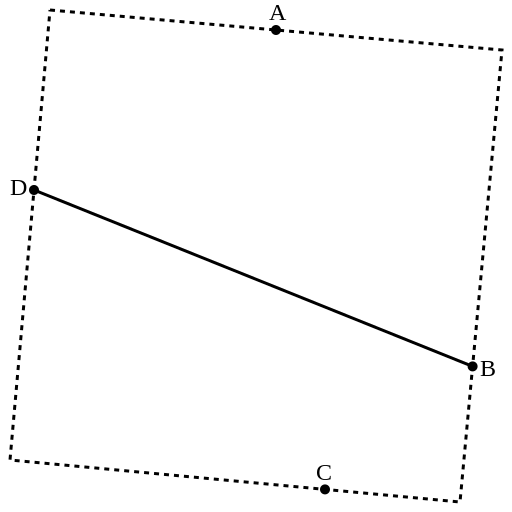
Опускаем перпендикуляр из точки A на прямую DB.
Отмечаем на этом перпендикуляре точку E так, что |AE|=|BD|. Точка E окажется на той же стороне квадрата, где точка C (или на продолжении этой стороны). После того, как мы определили ориентацию одной из сторон (линии CE), остаётся только опустить три оставшихся перпендикуляра, чтобы найти углы исходного квадрата.
Источник: еврейская задача №20 от Тани Ховановой (PDF).
То есть кто-то начертил квадрат, поставил на каждой стороне по одной точке (неизвестно в каком месте), потом квадрат стёр, но точки оставил. Задача — восстановить квадрат (найти его углы), используя обычные геометрические построения циркулем и линейкой.
Никаких подвохов, всё честно, для решения достаточно знания геометрии на уровне очень средней школы. Простое решение, которое сложно найти — под катом.
Выбираем две противоположные точки (в этом примере B и D) и соединяем их прямой.
Опускаем перпендикуляр из точки A на прямую DB.
Отмечаем на этом перпендикуляре точку E так, что |AE|=|BD|. Точка E окажется на той же стороне квадрата, где точка C (или на продолжении этой стороны). После того, как мы определили ориентацию одной из сторон (линии CE), остаётся только опустить три оставшихся перпендикуляра, чтобы найти углы исходного квадрата.
Источник: еврейская задача №20 от Тани Ховановой (PDF).
