Entry tags:
Недослучайные числа
А вот допустим приспичило мне определить π методом Монте-Карло. С кем не бывает. Дело нехитрое. Для начала надо надёргать пар случайных чисел, равномерно распределённых между 0 и 1. Примерно π/4 из них должны попасть в круг единичного радиуса с центром в начале координат. Можно посчитать процент попаданий в этот круг, умножить на 4 и получить таким образом оценку π.
Слышал я, что не все генераторы псевдослучайных чисел одинаково хороши, и некоторые из них норовят не очень случайные числа генерить. Поэтому на всякий случай смотрю на первые 256 точек.
На какой из двух картинок изображены равномерно распределённые псевдослучайные числа?


На первой картинке выхлоп std::default_random_engine через std::uniform_real_distribution из стандартной библиотеки GCC. Где густо, где пусто. И это нормально, равномерность у распределения только в пределе.
На второй картинке последовательность Халтона. Точки размазаны ровным слоем, но при этом не являются независимыми. Подобных квази-случайных последовательностей напридумывали много разных. Наиболее популярная — последовательность Соболя, но чтобы не лезть в дебри, обойдёмся Халтоном. В данном случае его достаточно.
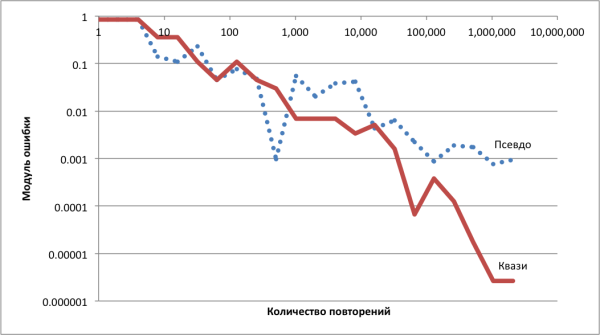
Смотрим, как себя ведёт ошибка при увеличении количества повторений.
Невооружённым глазом видно, что при использовании квазислучайной последовательности ошибка уменьшается заметно быстрее:
Слышал я, что не все генераторы псевдослучайных чисел одинаково хороши, и некоторые из них норовят не очень случайные числа генерить. Поэтому на всякий случай смотрю на первые 256 точек.
На какой из двух картинок изображены равномерно распределённые псевдослучайные числа?


На первой картинке выхлоп std::default_random_engine через std::uniform_real_distribution из стандартной библиотеки GCC. Где густо, где пусто. И это нормально, равномерность у распределения только в пределе.
На второй картинке последовательность Халтона. Точки размазаны ровным слоем, но при этом не являются независимыми. Подобных квази-случайных последовательностей напридумывали много разных. Наиболее популярная — последовательность Соболя, но чтобы не лезть в дебри, обойдёмся Халтоном. В данном случае его достаточно.
Смотрим, как себя ведёт ошибка при увеличении количества повторений.
#include <iostream>
#include <random>
double halton(unsigned index, unsigned base)
{
double f = 1, r = 0;
while (index) {
f /= base;
r += f * (index % base);
index /= base;
}
return r;
}
int main(void)
{
std::default_random_engine gen;
std::uniform_real_distribution<double> dist;
unsigned pseudo_count = 0, quasi_count = 0, next = 1;
std::cout << "N\tPseudo\tQuasi\n";
for (unsigned i = 1; i <= (1 << 21); i++) {
// Pseudo-random
double x = dist(gen), y = dist(gen);
if (x * x + y * y < 1) {
pseudo_count++;
}
// Quasi-random (Halton)
double a = halton(i, 2), b = halton(i, 3);
if (a * a + b * b < 1) {
quasi_count++;
}
// Results
if (i == next) {
std::cout << i
<< "\t" << 4. * pseudo_count / i
<< "\t" << 4. * quasi_count / i << "\n";
next <<= 1;
}
}
}
Невооружённым глазом видно, что при использовании квазислучайной последовательности ошибка уменьшается заметно быстрее:


no subject
Так это и есть равномерно
Соболь, например, из кода Грея получается. Чем дальше в лес, тем больше битов. При этом в любой момент весь интервал оказывается покрыт равномерно.
RE: Так это и есть равномерно
А какой спектр нужен?
Подозреваю, что Соболь (или по крайней мере большинство его потоков) выдаёт более-менее ровный спектр. Особенно если начало последовательности пропустить.
А аддитивный генератор (следующая точка = предыдущая точка плюс иррациональная константа по модулю 1) будет выдавать узкий пик.
Re: А какой спектр нужен?